摘要

近年来，随着涡旋光束和空间结构光场的发展或应用，涡旋光束轨道角动量（OAM）的检

测成为重要的课题。本文基于空间光调制器（SLM）的全息衍射光栅方法，通过设计强度

分布和衍射角可调的衍射光栅对单模涡旋光束的OAM进行检测。课题组首先从自行设计的

一维全息衍射光栅开始进行验证，然后设计了二维全息衍射光栅，成功探测到单模涡旋光

束的OAM。理论和实验非常一致。该方法对基于SLM的全息衍射光栅的设计具有参考价值，

对基于涡旋光束的OAM检测和数据传输系统具有参考价值。

引言

由于涡旋光束和结构化光场的发展和应用，涡旋光束OAM的检测成为近年来的重要课题。

涡旋光束是相位因子为exp(ilφ)的光场，其中l是拓扑电荷，φ是方位角。涡旋光束中的每

个光子都携带lħ（ħ是普朗克常数）OAM。涡旋光束在光镊、产生矢量光束、冷原子引导

等各个领域得到了广泛的应用和研究。轨道角动量是涡旋光束和结构光场的新维度。它的

调制能力和信道容量远优于普通高斯光束。因此，轨道角动量的检测和拓扑电荷的确定是

一个关键问题。课题组在本文中给出了一种检测涡旋光束轨道角动量的方法，该方法是基

于空间光调制器（SLM）的衍射光栅方法。

一维和二维全息图像的理论模型

对于一维全息光栅的设计，必须确定一维连续的仅相位函数。这个相位函数可以产生所需

要的衍射级数，可以傅里叶展开为：

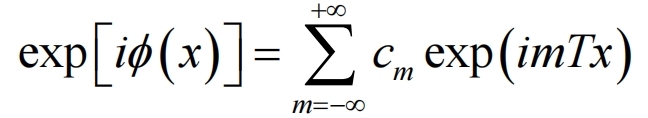
式1

其中m是衍射级数，T是光栅常数。上述方程中的傅里叶系数cm为：

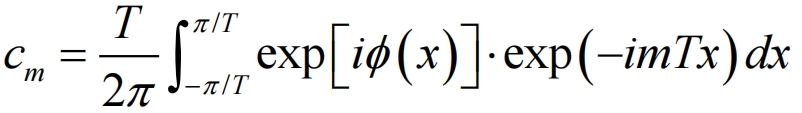
式2

通常，上述方程中的系数是相位光栅产生的每个衍射级的复幅值，可以表示为：

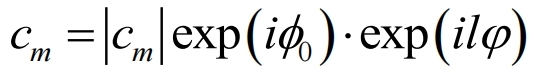
式3

其中ǀcmǀ是振幅，Φ0是初始相位，l是拓扑电荷，φ是方位角。应该注意的是，方程（1）的

左侧必须是二维的，因为右侧项包括方位角坐标。方程（2）和（3）表明可以定义所需的目

标阶数m、所需的振幅 ǀcmǀ、初始相位Φ0和拓扑电荷l。然后可以通过方程（1）获得光栅

的相位分布函数，它可以产生一维光学涡旋阵列称之为一维编码全息光栅。图 1（b）显示

了所设计的一维光栅。当高斯光束入射时，其远场衍射图样有两个-1级和+1级的光斑，拓

扑电荷分别为+1和+2。

图 1.（a）高斯光束的强度分布;（b）设计的1D全息光栅;（c）入射到所设计的一维全息光栅上的高斯光束

远场强度分布的理论模拟;（d）实验结果。

将衍射光栅扩展到二维。为了生成二维涡旋光束阵列，可以使用一种将轴向和两个正交编码

全息光栅相结合的方法，并且易于理解。在x方向上的编码全息光栅是方程（1）和方程 （3）

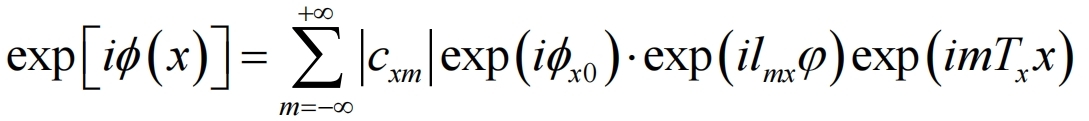
式4

同理，编码全息光栅在 y 方向上的表达式为：

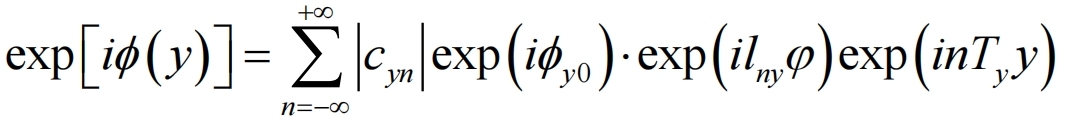
式5

组合方程。（4）和（5）中，二维编码的全息光栅写为：

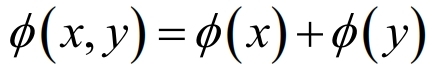
式6

当高斯光束入射到二维编码全息光栅上时，如方程（6）所示，将产生二维光学涡旋阵列。

衍射光斑中衍射级数（m，n）的拓扑电荷与lmx和lny有关，可以写成lm，n=（lmx+lny）。

请注意，如果缺少每个一维数组的m或n阶数（ǀcxmǀ=0或ǀcymǀ=0），由于二维数组是一

维数组的扩展，因此二维数组中的阶数（m，n）将不存在。

实验结果

如图2所示。LD激光器通过透镜L1和L2展开和准直。然后，偏振分束器（PBS）将光束调

整为水平偏振。SLM1是产生具有所需拓扑电荷的涡旋光束，并将产生的涡旋光束照射到

SLM2进行解调，因此SLM2需要加载设计的2D光栅。需要在两个SLM之间添加一个由两

个镜头L3和一个针孔组成的4-f系统，以进行空间过滤。最后，SLM2反射的光束穿过透镜

L4进行聚焦，傅里叶变换光场以观察远场衍射图样。激光束分析仪（LBA）放置在镜头L4

的焦平面。

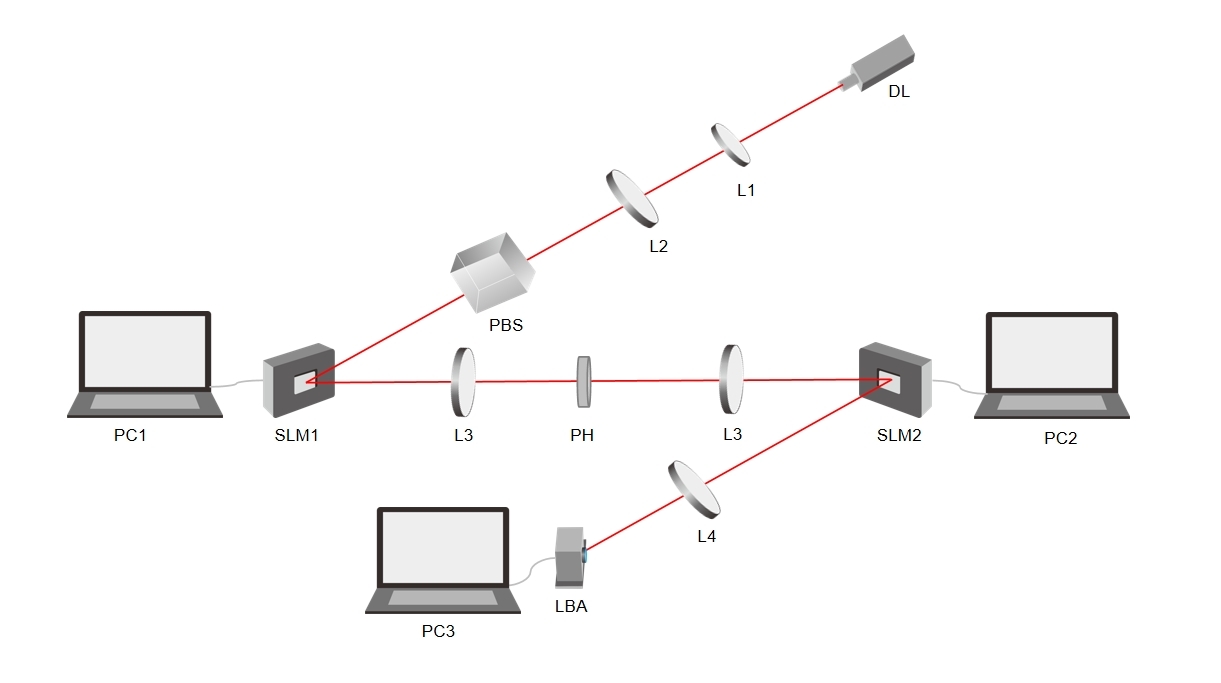
图 2.实验图

课题组设计了一个二维编码的全息光栅，将其加载到SLM2上。当SLM1上没有加载光栅时，

即当高斯光束入射光栅时，其远场衍射图谱将产生一个2×2的涡旋阵列，拓扑电荷分别为-3、

-1、1 和3，如图3所示。图3（b）显示了2D编码全息光栅的相位分布，图3（b）显示了2D

编码全息光栅的相位分布。图3（c）和图3（d）分别是高斯光束入射光栅后远场衍射图谱的

理论模拟和实验结果。从图3中可以观察到，实验和理论非常一致。

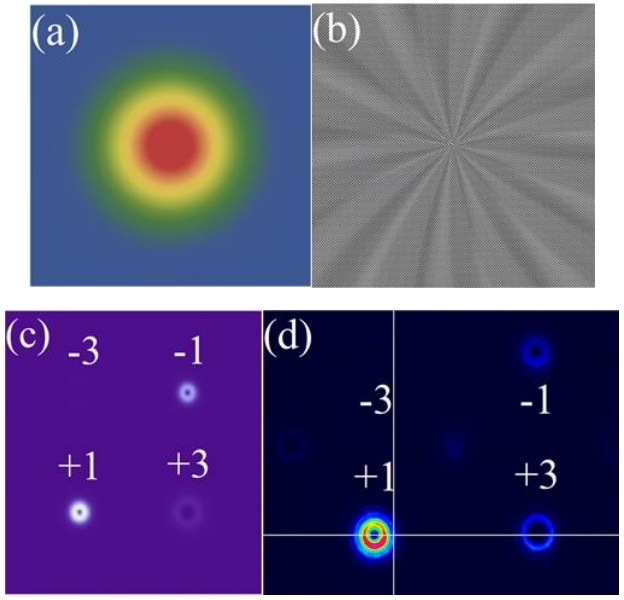
图 3.（a）高斯光束的强度分布;（b）设计的2D全息光栅;（c）入射到所设计的二维全息光栅上的高斯光束远场

强度分布的理论模拟;（d）实验结果。

图4显示了涡旋光束的远场衍射图，拓扑电荷为-1和-3进入二维编码全息光栅。

图4（d）和（e）是分别入射到二维编码全息光栅上的拓扑电荷为-1和-3的涡旋光束的远场衍射图。

如图中红色圆圈标记点。可以观察到，当拓扑电荷为-1的涡旋光束照射光栅时，衍射图的左下角会

出现高斯光斑。由于图3中的这个位置会产生拓扑电荷为+1的涡旋光束，因此拓扑电荷在此位置抵

消，并出现高斯光斑。同样，这个结果也可以在图4（e）中观察到。因此，实验和理论非常一致。

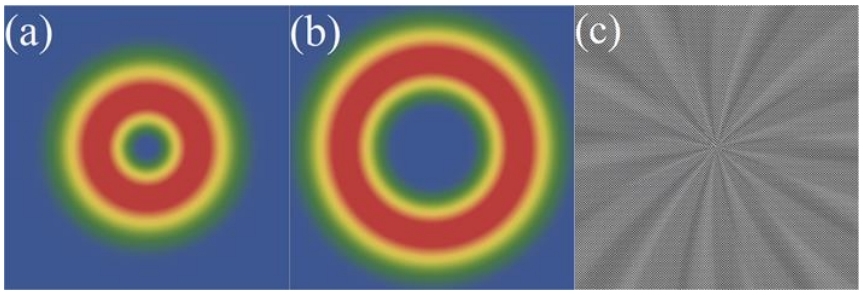
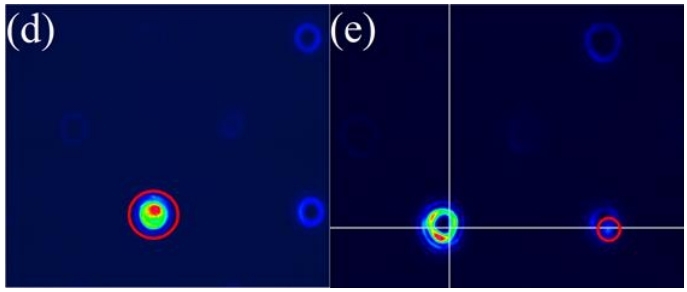
图 4.（a）拓扑电荷为 -1 的涡旋光束强度分布;（b）拓扑电荷 -3 的涡旋光束强度分布;（c）设计的 2D 全息光栅;

（d）拓扑电荷 -1 入射的涡旋光束在所设计的二维全息光栅上的远场强度分布的实验结果;（e）拓扑电荷 -3 入射

到所设计的二维全息光栅上的涡旋光束远场强度分布的实验结果

论文信息

论文信息：

Wang, Y., Bai, L., Xie, J., & Guo, Y. (2021). Orbital angular momentum detection of vortex

beam based on diffraction grating. Sixteenth National Conference on Laser Technology

and Optoelectronics.

DOI:10.1117/12.2601810